Deep Dive into Database Design - Part 2

Mastering Advanced Concepts and Best Practices in Database Architecture

This is the second part of a two-part guide on database design.

Recall that this guide is split into two sections:

• Part 1 covers database systems, database design and the relational model. Examples are provided to explore the different aspects of these topics in detail. 

• Part 2 covers the database design refinement process. Once we’ve achieved an initial design, the objective becomes to maintain data integrity and constraints while maximally eliminating redundancy.

Contents 

1. Part 1 (This Post) - Initial Database Design

   • Introduction to database systems

   • Database design

   • The relational model

2. Part 2 (Next Post) - Normalization and Refined Database Design

   • Schema normalization 

   • Schema refinement 

   • Functional dependencies

   • Normal forms

   • Going Deeper - BCNF

   • Going Deeper - 3NF

   • Properties of decompositions

   • Normalization

   • Synthesis 

---

Section 1 - Schema normalization

• Schema normalization is the process in database design used to organize databases into tables and column iteratively, once we have defined our first set of tables/columns

• The purpose of this continued iterative approach is to reduce redundancy and improve data integrity

• The focus is on breaking down large tables into smaller, more manageable tables 

• The objective is to (1) minimize duplication while (2) enduring data dependencies are consistent 

Normalization Steps

• There are ‘levels’ in normalization that you can reach in the amount of normalization that you have done

• Each level is referred to as a normal form

• Each level also must abide by a set of rigorous rules - which is what classifies it being at that “level”

Normal Forms

1. First Normal Form (1NF)

   • Every table must have a primary key 

   • Each table must only have column contains only atomic (indivisible) values (no lists or arrays)

   • Repeating groups or arrays are not allowed

2. Second Normal Form (2NF)

   • Builds on 1NF 

   • All non-key columns are fully functionally dependent on the primary key - this means that each non-key column must be related to the whole primary key, not just part of it - we’ll look at examples 

3. Third Normal Form (3NF)

   • Builds on 2NF 

   • Every non-key column is (1) not only dependent on the primary key but also (2) independent of each other - this eliminates transitive dependencies, where one non-key column depends on another non-key column - 

4. Boyce-Codd Normal Form (BCNF)

   • A stronger version of 3NF

   • BCNF requires that every determinant (a column or a set of columns on which some other column is fully functionally dependent) is a candidate key

   • It deals with certain anomalies that 3NF does not address

There are also other normal forms that will not be addressed:

1. Fourth Normal Form (4NF)

2. Fifth Normal Form (5NF)

If you don’t understand some of these definitions now, they will soon be addressed with more refined definitions and examples in the following sections.

It is recommended in most practical production databases that 2NF/3NF is met.

A conceptual database design gives us a set of relation schemas and ICs 

• The initial design can be refined by taking the ICs as a conceptual schema produces by translating the ER model design into a collection of relations

There are a set of constraints called functional dependencies.

There are also multivalued dependencies and join dependencies.

---

Section 2 - Schema refinement 

Redundancy 

Redundancy refers to the following problems in databases: 

• Redundant storage of information 

• Update anomalies

  • If one copy of repeated data is updated, an inconsistency is created unless all copies are updated 

• Insertion anomalies

  • It may not be possible to store certain information unless some other information is also stored

• Deletion anomalies 

  • It may not be possible to delete certain information unless some other information is also stored

Example

Hourly_Employees (ssn, name, lot, rating, hourly_wages, hours_worked)
Hourly_Employees (S, N, L, R, W, H)

Suppose that hourly_wages is determined by rating: 

• This means that for some rating, the hourly_wages value is always the same

• This IC is an example of a functional dependency and leads to possible redundancy

  • For this table, we don’t need to record hourly_wages for each item since we know what the hourly_wage is for a given rating - if it changed, we would need to update all records 

Decompositions

We address this through the analysis of our database using a quasi-mathematical language:

• Functional dependencies (FDs) are dependencies that we define between attributes

• FDs be used to identify situations of redundancy

• Identifying redundancy, then, can allow us to replace larger tables with smaller tables 

• Simply put: a decomposition is the process of replacing large unoptimized tables with smaller optimized tables inside our database in order to reduce or eliminate redundancy 

A decomposition of a relation schema R consists of replacing the relation schema by two (or more) relation schemas that each contain a subset of the attributes in R and together include all attributes in R.

• We want to store the information in any given instance of R by storing projections of the instance 

Example decomposition

Recall our initial table in Example 1:

Hourly_Employees (ssn, name, lot, rating, hourly_wages, hours_worked)
Hourly_Employees (S, N, L, R, W, H)

Hourly_Employees can be decomposed into:

• Hourly_Employees_Main (ssn, name, lot, rating, hours_worked)

• Wages (rating, hourly_wages)

At this point, we’ve illustrated a decomposition without showcasing how to do it - we’ll address that point 2 soon.

Questions to address related to decomposition 

1. How do we know if we need to decompose a relation?

2. Given that decomposition alters our database design, what side-effects / problems are created?

Question 1

• As specified earlier, levels of ‘integrity’ have been formally defined - known as normal forms

• Each of these normal forms guarantee:

  • A certain amount of normalization and lack of redundancy, related to targeted scenarios 

  • A logical check where certain problems cannot arise

• Therefore, in order to prevent certain problems or scenarios, we can select a depth, a normal form, as a milestone for our database design

Question 2

When decompositions, we will look at two primary properties:

1. Lossless-join

   • The opposite of decomposition is synthesis - which is when we re-compose our decomposed relations back into their original form

   • In synthesis, a relation can either be losses or lossy - which refers to whether the original information is completely preserved or partially lost in the decomposition process

   • A lossless join is a property of a decomposed relation

   • A lossless join is true to exist if we can recover all instances of the decomposed relation from the instances of the smaller relations 

2. Dependency-preservation 

   • Enforce all constraints on the original relation by enforcing the same constraints on each of the smaller relations - that is, to not perform any joins in order to check constraints 

---

Section 3 - Functional dependencies (FDs)

• A functional dependency is a kind of integrity constraint

• They describe a relationship between different attributes in a database table

• A FD occurs when one attribute uniquely determines another

Example

Consider a table Students with attributes StudentID, StudentName, and Email:

• If StudentID uniquely determines StudentName and Email, then we have two functional dependencies:

  • StudentID → StudentName, and 

  • StudentID → Email 

Formal Definition

Let R be a relation schema. 
Let X and Y be non-empty sets of attributes of R.

An instance r of R satisfies FD (X → Y) if the following holds for every pair of types t1 and t2 in r:

• If (t1.X = t2.X), then (t1.Y = t2.Y)

This is stating that R is some table, and X and Y are lists of attributes. R ‘satisfies’ a FD (X → Y) if:

• For every X column value (for every row), you get the Y column value 

• “If two types agree on the values in attributes X, then they must agree on the values in attributes Y)”

Example

FD: AB → C

• The combination of column values (A, B) together (for every record) always gives you the column values C

A legal instance of a relation must satisfy all ICs, including all specified FDs.

A primary key constraint is a special case of an FD

• The attributes in the key play the role of X

• The set of all attributes in the relation plays the role of Y

• However, the FD definition does not require that the set of X be minimal

  • This is an additional condition for a key

If X → Y holds, where Y is the set of all attributes and there is some subset V of X such that V →  Y holds, then X is a superkey (and not a key, since keys are minimal and there would be no subset).

Example

• There are some FDs that hold over R.

• ssn to did holds since ssn is the primary key in this relationship relation and did is a FK

• There are also implied FDs, such as: ssn → did

R = Workers (S, N, L, D, S)

F = FDs = {
  ssn → did,
  did → lot
}

Closure of a Set of FDs

A set of all FDs implied by a given set F of FDs is called the closure of F (F⁺)

How can we infer / compute the closure of a given set of F?

• There are three rules, called Armstrong’s Axioms that can be applied repeatedly to infer all FDs

Armstrong’s Axioms

Let X,  Y, and Z denote sets of attributes over a relation schema R:

1. Reflexivity

   • If Y ⊆ X, then X → Y

2. Augmentation

   • If X → Y, then XZ → YZ for any Z

3. Transitivity

   • If X → Y and Y → Z, then X → Z

Theorem 1 

1. AAs are sound: they generate only FDs in F⁺ when applied to a set F of FDs

2. AAs are complete: their repeated application will generate all the FDs in F⁺

Attribute Closure

How do we check if a dependency (X → Y) is in the closure of a set F of FDs?

1. You can compute the closure of F and see if this dependency is inside; or

2. We can find out without computing the closure of F.

How?

Compute the attribute closure of X with respect to F 

The set of attributes A such that X → A can be inferred using the Armstrong Axioms

Algorithm: 

closure = X

Repeat until there is no change: {
  If (there is an FD U → V in F such that U ⊆ closure):
  Then (set closure = closure U V)
}

Theorem 2

The algorithm above computes the attribute closure of X with respect to a set of FDs called F.

---

Section 4 - Normal forms 

For decomposition, it will be guided by an understanding of what problems (if any) arise from the current schema.

Several normal forms exist that guarantee that different problems cannot arise:

1. First normal form (1NF)

2. Second normal form (2NF)

3. Third normal form (3NF)

4. Boyce-Codd normal form (BCNF)

Each normal form has increasingly restrictive requirements.

• Every relation “in” BCNF is also “in” 3NF and also “in” 2NF and also in “1NF”

• Every relation “in” 3NF is also “in” 2NF … and so on ..

1NF

• A relation is in 1NF if every field contains only atomic values (no lists or sets exist)

• In the relational model, this is already implicit in the definition 

• Some newer database systems are relaxing this requirement

2NF

• 2NF is mainly of historical interest, and 3NF and BCNF are important from a database design perspective

• All the column depend on the primary key (there are no partial dependencies)

3NF

• All the columns are not transitively dependent on the PK

This means all non-key attributes are functionally dependent upon the PK

• All fields (attributes) should be dependent on the tables’ PK

• If they are not, they should not be put in this table 

---

Section 5 - Going Deeper - BCNF

Definition 

Let R be a relation schema
Let F be a set of FDs given to hold over R
Let X be a subset of attributes of R
Let A be an attribute of R

A relation is in BCNF if every determinant is a candidate key

• Don’t have PK made up of more than one field unless it is a join table to disperse a many to many relationship and only contains the 2 PKs of the table it is joining 

R is in BCNF if, for every FD (X →  A) in F, one of the following is true:

• A is an element in X (it is a trivial FD); or

• X is a superkey 

A superkey is a set of attributes that can uniquely identify each record.

A candidate key is the minimal set of attributes in a superkey. And there can be multiple candidate keys.

Each attribute must describe (an entity or relationship identifier by) the key, the whole key, and nothing but the key.

BCNF ensures that no redundancy can be detected using FD information alone.

If a relation is in BCNF, every field of every tuple records a piece of information that cannot be inferred (using only FDs) from the values in all other fields in (all tuples of) the relation instance.

---

Section 6 - Going Deeper - 3NF

Definition 

Let R be a relation schema.

Let F be the set of FDs given to hold over R.

R is in 3NF if, for every FD (X → A) in F, one of the following statements is true:

• A is an element of X (thus a trivial FD), or

• X is a superkey, or

• A is part of some key for R

Requires all columns to be dependent only upon the PK.

All non-key attributes are functionally dependent only upon the PK.

• All fields should be dependent on the tables PK

• If they are not, they should be put in their own table 

• Unless each attribute is a PK or FK attribute, it must be directly dependent on the PK and not some other attribute 

Third condition explained:

• Recall that a key for a relation is a minimal set of attributes that uniquely determines all other attributes

• A must be part of a key (not enough for A to be part of a superkey)

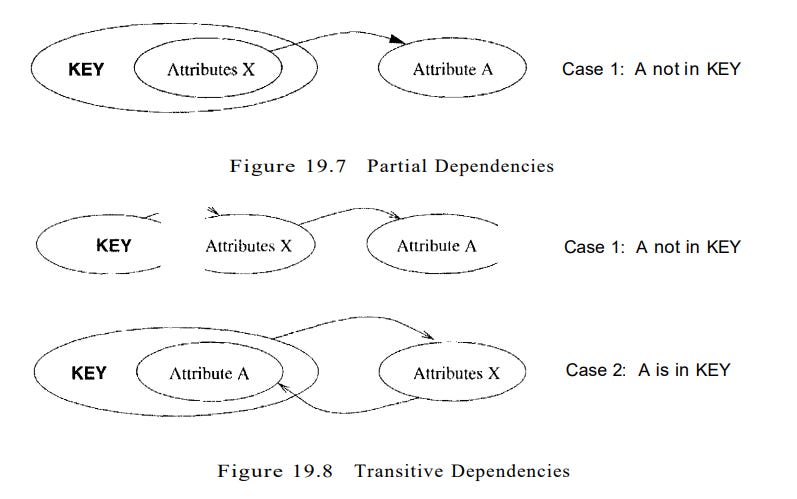
Suppose that a dependency X → A causes a violation of 3NF - two cases exist:

• X is a proper subset of some key K

  • This is called a partial dependency

  • We store (X, A) pairs redundantly 

• X is not a proper subset of any key

  • Called a transitive dependency

  • This means we have a chain of dependencies, such as K → X → A

---

Section 7 - Properties of Decompositions

Properties 

1. Lossless-join

2. Dependency-preservation

5.1 | Lossless join

Let R be a relation schema and let F be a set of FDs over R.

A decomposition of R into two schemas with attribute sets X and Y is said to be a lossless-join decomposition with respect to F if:  for every instance r of R that satisfies the dependencies in F:

π_X (r) ⨝ π_Y (r) = R

• The join of - the projection of X (attributes set of r) and the projection of Y (attributes set of r) - equals R

• The equijoin, which means joining an elements that match

In other words, we can recover the original relation from the decomposed relations.

Then this definition is extended to cover a decomposition of N sub-relations.

All decompositions to eliminate redundancy must be lossless.

Theorem 3

Let R be a relation and F the set of FDs that hold over r. Let R1 and R2 be attribute sets.

R decomposed into R1 and R2 is lossless if and only if F+ contains either:

1. The FD: (R1 ∩ R2) → R1, or 

2. The FD: (R1 ∩ R2) → R2

The attributes common to R1 and R2 must contain a key for either R1 or R2.

In a lossless decomposition, we select the common attribute that must be a candidate key or a superkey of either R1, R2, or both.

It is a lossless-join decomposition if at least one of the two functional dependencies are in F+:

1. (R1 ∩ R2) → R1

2. (R1 ∩ R2) → R2

Example

R (ABCD)
FDs = {
  A → B, 
  B → C,
  C → D,
  D → B
}

R1 (AB)
R2 (BC)
R3 (BD)

R1: (Intersection (R1, R2, R3) = B) → AB
R2: (Intersection (R1, R2, R3) = B) → BC
R3: (Intersection (R1, R2, R3) = B) → BD

B → C is true. Therefore it is a lossless join

Is this a lossless-join? Is it dependency preserving?

Example

R(SNLRWH) has a violation of 3NF therefore it is split into R1(SNLRH) and R2(RW)

Since R is common to both decomposed relations and R → W holds, the decomposition is a lossless join.

5.2 | Dependency preservation

• If you split up R into sub-relations and you cannot check certain dependencies without a join, then it is not dependency preserving.

• A dependency-preserving decomposition allows us to enforce all FDs by examining a single relation instance on each insertion or modification of a record

For dependency-preserving decompositions, you need the projection of FDs.

Let R be a relation schema that is decomposed into two schemas with attribute sets X and Y.
Let F be the set of FDs over R

The projection of X on X is the set of Fds in the closure F_X that involve only the attributes in X

• The projection of F on attributes X is F_X

• A  dependency U → V in F+ is in F_X only if all attributes in U and U are in X

The decomposition of R with FDs F into schemas with attribute sets X and Y is dependency-preserving if (F_X U F_Y)⁺ = F⁺

• If we take the dependencies in F_X and F_Y and compute the closure of their union, we must get back all the dependencies in the closure of F

Therefore: 

To enforce F_X, we only need to examine the relation X on inserts and likewise with Y.

Example

R (ABC)

FDs = { 
  A → B,
  B → C,
  C → A
}

Suppose we split them into R1(AB) and R2(BC).

FAB = { A → B }
FBC = { B → C }
F+ = { A → B, A → C, B → C, B → A, C → A, C → B }

Therefore - there are some ‘hidden’ dependencies that we add to F_AB and F_BC that we found with the closure.

FAB = { A → B, B → A }
FBC = { B → C, C → B }

FAB U FBC = { A → B, B → A, B → C, C → B }
(FAB U FBC)+ = { A → B, A → C, B → C, B → A, C → A, C → B }

Therefore, this composition is dependency preserving.

---

Section 8 - Normalization

BCNF

• Obtain a lossless-join decomposition into a collection of BCNF relation schemas.

• In some cases, there may be no dependency-preserving decomposition into a collection of BCNF

Decomposition into BCNF

Starting with relation R and FDs F.

1 | Suppose that R is not in BCNF (check BCNF):

Let X ∈ R.

Let A be a single attribute in R.

Let X → A be a FD that causes a violation of BCNF

• A cannot be in X since it is a trivial dependency 

• X is not a superkey

• Therefore X ∩ A is empty and each composition is a lossless-join.

What to do? Decompose R into R1 (R - A) and R2 (XA)

2 | If either (R - A) or (XA) are not in BCNF, decompose further by the recursive application of this decomposition.

You can arrive at different collections of BCNF relations based on what you choose to split on.

3NF

• Always dependency-preserving

• Always lossless-join 

Decomposing into 3NF

Before the algorithm, you need the concept of a minimal cover for a set of FDs:

A minimal cover for a set of FDs F is a minimal set G of FDs such that:

1. Every dependency in G is in the form, X → A, where A is a single attribute

2. The closure of F (F+) = The closure in G (G+)

3. If we obtain a set H of dependencies from G by deleting one or more dependencies (or by deleting attributes from a dependency in G), then F+ does not equal H+

It is minimal in two respects:

1. Every dependency is as small as possible 

   • Each attribute on the left side is necessary 

   • The right side is a single attribute

2. Every dependency is required for the closure G+ to be equal to F+

General algorithm for the minimal cover

1. Put the FDs in standard form - obtain a collection G of equivalent FDs with a single attribute on the right side 

   • Using the Decomposition axiom

2. Minimize the left side of each FD:

   • For each FD in G, check each attribute in the left side to see if it can be deleted while preserving equivalence to F+

3. Delete redundant FDs:

   • Check each remaining FD in G to see if it can be deleted while preserving equivalence to F+

You must minimize the left side of FDs before checking for redundant FDs.

Process

1. Get the RHS to a single attribute

2. For double LHS items:

   • Compute the closure of each item on the left. If you can obtain the other attributes from one of the attribute, remove the attributes that are ‘redundant’ (that you can get without it on the LHS)

3. For FD x_i = X → A dependency:

   • If you can get A from X+ without x_i, then remove this dependency because it is redundant 

Dependency-Preserving Decomposition into 3NF 

The goal is to obtain a (1) lossless-join, (2) dependency-preserving decomposition into 3NF relations.

Let R be a relation with the set of G of FDs that is a minimal cover.
Let R1 to Rn be a lossless-join decomposition of R. 

Suppose each R_i is in 3NF and let F_i be the projection of F onto the attributes of R_i.

Do the following:

1. Identify the set N of dependencies in F that are not preserved (not included in the closure of the union of F_i)

2. For each FD (X → A) in N, create a relation schema XA and add it to the decomposition of R.

Every dependency in F is preserved if we replace R by the R_i plus the schema of the form R (XA)

• The R_i are given to be in 3NF

Why each R (XA) is in 3NF:

Since X → A is in the minimal cover of F, Y → A does not hold for any Y that is a strict subset of X.

Therefore X is a key for XA.

If any other dependencies hold over XA, the right side can involve only attributes in X because A is a single attribute.

Therefore since X is a key for XA, none of these additional dependencies cause a violation of 3NF.

---

Section 9 - Synthesis 

3NF Synthesis

Our FDs are to guide decisions about decomposition

• A lossless-join 3NF decomposition is straightforward

• The algorithm addresses dependency-preservation by adding the additional schemas (XA)

• There is an alternative approach called synthesis

Synthesis

Take all the attributes over the original schema R and the minimal cover of F.

Add a relation XA to the decomposition of R for each FD (X → A) in F.

The resulting collection is in 3NF and preserves all FDs.

• If it is not a lossless-join, we can make it by adding a relation schema that contains only those attributes that appear in some key

• Therefore the full algorithm can arrive at a lossless-join, dependency-preserving decomposition into 3NF

---